En este artículo, explicaré como calcular las sobrepresiones que se producen cuando se cierra rápidamente una válvula en conducciones a presión por gravedad.

Si el agua se mueve por una tubería con una velocidad determinada y mediante una válvula se le corta el paso totalmente, el agua más próxima a la válvula se detendrá bruscamente y será empujada por la que viene detrás. Se inicia entonces un proceso de compresión ya que la energía cinética del agua se transforma en energía de compresión. A partir de aquí el movimiento del agua se transformará en un movimiento oscilatorio (compresión y descompresión) hasta que se alcance el equilibrio estático. Este movimiento oscilatorio es el que da lugar al golpe de ariete (ruido parecido a un martilleo) y puede llegar a producir la rotura de la conducción y desperfectos en otros mecanismos. El procedimiento de cálculo de la sobrepresión generada es como sigue.

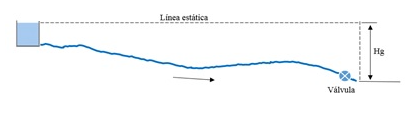
En primer lugar se obtiene la celeridad de la onda de presión. Esta velocidad de onda se calcula mediante la conocida fórmula:

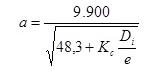
Siendo:

Di el diámetro interior de la tubería en mm

e, el espesor de la tubería en mm

Kc es un parámetro adimensional, calculado a partir de la expresión:

Donde E es el módulo de elasticidad del material de la tubería en kg/m2

A continuación se calcula el tiempo crítico, tc, el cual representa el tiempo (en segundos) que tarda la onda en recorrer un ciclo entero, es decir, una ida y vuelta completa por la tubería, siendo independiente este valor de la forma en que se produzca el cierre.

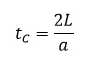
L es la longitud de la conducción en metros, a la celeridad en m/s.

La comparación del tiempo de maniobra (tM) –o tiempo de cierre de la válvula de corte- con este tiempo crítico nos va a permitir diferenciar un cierre lento de un cierre rápido.

Si tM ≥ tc consideraremos el cierre lento, y el caso contrario (tM < tc) será cierre rápido.

Se determina seguidamente el valor máximo de la sobrepresión.

Para cierres lentos aplicaremos la ecuación de Michaud:

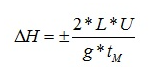
En la que U es la velocidad de circulación del agua. Los demás parámetros son ya conocidos.

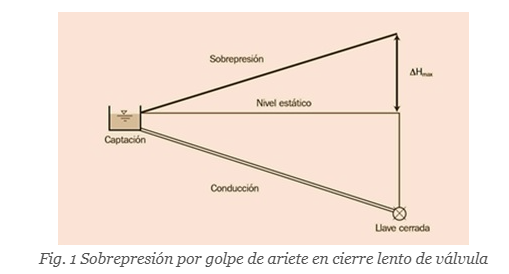
En la gráfica siguiente vemos la línea de sobrepresiones debida a un cierre lento de válvula.

Para cierres rápidos aplicaremos la ecuación de Allievi:

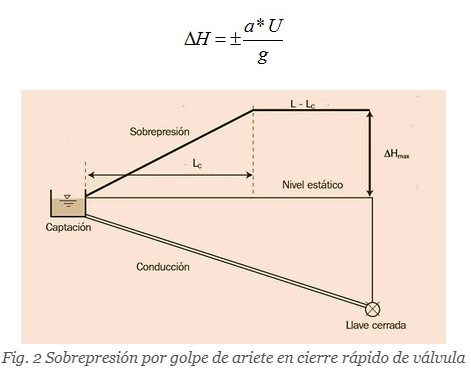
En el caso de los cierres rápidos, la sobrepresión alcanza igualmente su valor máximo en la válvula que se cierra  pero, como muestra la figura 2 (línea gruesa continua), ésta se mantiene en una longitud de tubería igual a L-Lc, lugar a partir del cual disminuye hasta reducirse a cero (el punto donde comienza a disminuir la sobrepresión se denomina punto crítico). A partir de este punto y hasta el origen (distancia a la que se denomina longitud crítica, Lc), el cálculo de la sobrepresión se realizará mediante la fórmula de Michaud. Por tanto para los cierres rápidos se emplearía para el cálculo de las sobrepresiones en la conducción ambas fórmulas.

El valor de la longitud crítica, en metros, está dado por la expresión:

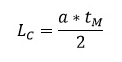
Finalmente deberemos considerar los valores de presión máxima y mínima soportada por la tubería y comprobar si la tubería tiene capacidad para resistirlo. La máxima presión soportada por la tubería será la suma de la sobrepresión por golpe de ariete (∆H) y la presión estática (Hg). La suma de ambas deberá de ser inferior a la presión máxima admisible por el tubo.

Veamos a continuación un ejemplo de cálculo para comprender lo explicado.

Se diseña una conducción por gravedad de 820 metros de longitud en cuyo tramo final se encuentra una válvula para dar servicio a unas parcelas de riego. El tubo es de PE100 de 160 mm de diámetro y presión nominal de 10 bar fabricado según norma UNE-EN 12201. El espesor de la pared del tubo es de 9,5 mm. La presión máxima admisible es igual a la presión nominal. La presión estática: 65 metros. El tiempo de cierre de la válvula: 5 segundos. Calcular la sobrepresión así como el tiempo de cierre que se debería dar a la válvula para evitar un golpe de ariete, suponiendo que por la tubería circulará un caudal máximo de 43 l/s

Datos: L: 820 m   DN: 160 mm   PN: 10 bar   Q: 43 l/s   TM: 5 s   Hg: 65 m

* Calculamos la celeridad de la onda:

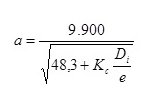
El espesor e = 9,5 mm; diámetro interior = 141 mm

El módulo de elasticidad del PE100 es E = 1*10^8 kg/m2, por tanto Kc = 100 kg/m2

La celeridad a = 253 m/s

* Obtenemos el tiempo crítico:

​​La longitud de la conducción L= 820 m

La celeridad de la onda a = 253 m/s

El tiempo crítico, tc = 6,5 segundos > tM (5 segundos). Se trata de un cierre rápido.

* Aplicamos fórmula de Allievi:

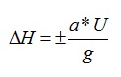
La velocidad de circulación del agua v=Q/S = 0,043 / 0,0156 = 2,8 m/s

∆H = +72 mca.

* Deducimos la presión máxima soportada por la tubería.

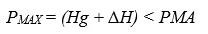
Ht= PMAX= 65 + 72 = 140 mca > 100 mca (PMA)

La sobrepresión generada supera la capacidad de resistencia de la tubería.

Deduciremos de la ecuación de Michaud el tiempo de cierre para convertir la maniobra en un cierre lento:

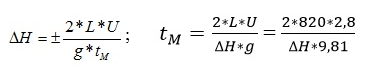
¿Qué valor de ∆H consideraremos aceptable en la fórmula anterior? Aquél que sumado a la presión estática sea igual o inferior a 100 mca, que es la presión máxima admisible del tubo. Por tanto:

∆H + Hg ≤ 100 mca; ∆H + 65 ≤ 100 mca; ∆H = 35 mca

Sustituimos en la expresión y obtenemos el tM o tiempo de cierre de la válvula para evitar el problema de la sobrepresión.

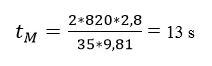
Por último comentar que el valor del golpe de ariete dependerá normalmente de los siguientes factores:

• Velocidad del agua. Para evitar la sobrepresión se limitan las velocidades de circulación del agua a un máximo de 3 m/s en conducciones por gravedad.
• Longitud de la conducción. A mayor longitud de tubería mayor será el golpe de ariete debido al aumento de energía cinética de la masa líquida en movimiento.
• Material de la tubería. Dependiendo de la elasticidad del material con el que esté fabricada la tubería podrá absorber en mayor medida las ondas derivadas del golpe de ariete.T
• Tiempo de maniobra tM o tiempo que se ocupa en abrir o cerrar una válvula. 

Nota: