Cuando se trata de tubos, claro que importa. El diámetro de un tubo en una impulsión y el costo energético del bombeo van de la mano.  Cuando eliges el diámetro de una tubería para una impulsión debes de considerar, además del costo de instalación del tubo, el costo energético que supone bombear una cantidad determinada de agua durante el periodo anual de funcionamiento de la instalación. Bien, en este post verás un nuevo concepto, el de velocidad económica, que está relacionado directamente con el costo energético del bombeo y, por tanto, con la sección de la conducción.

Un diámetro de tubo menor conlleva menores costos de instalación, pero mayores pérdidas en la explotación debidas al incremento del costo energético causado por las pérdidas de presión en la red.

Este post es un homenaje al profesor D. José Agüera Soriano, al que lamentablemente no tuve el placer de conocer. El profesor Agüera Soriano, jienense de nacimiento, pasó toda su vida en Córdoba (España) ligado a la Universidad, su verdadera pasión, en la que fue profesor de Hidráulica y Termodinámica, Gerente, Catedrático de la Escuela Universitaria de Mecánica de Fluidos, de Termodinámica y Motores Térmicos y profesor emérito. Publicó varios libros técnicos docentes sobre Termodinámica, Motores y Mecánica de Fluidos.

El Sr. Agüera trabajó en la obtención de una fórmula para el cálculo de diámetros económicos en impulsiones que conjugase tres tipos de costos:

1. Los debidos a la tubería instalada,
2. Los derivados del costo de la bomba,
3. Los costos del importe actualizado de la energía eléctrica a pagar en t años de vida útil de la instalación.

Partiendo de las expresiones de diámetro económico de Mendiluce, Melzer y Vibert y utilizando un factor de actualización de la energía, llegó a una expresión cuya fórmula simplificada para el cálculo del diámetro económico en una impulsión es la siguiente:

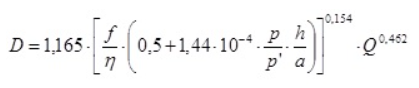
En la cual:

D, es el diámetro del tubo en metros.

f, el factor de fricción de la tubería

η, el rendimiento de la bomba.

h, es el número de horas de funcionamiento de la bomba al año.

Q, es el caudal bombeado en m3/s

a, es el factor de actualización, inverso al factor de amortización, y se calcula como:

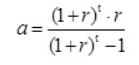
en el que r es el interés real del dinero (promedio 3% en España) y t el número de años de vida útil (se toma 25 años); por tanto para estos datos a = 0,057

p/p’ expresa la relación entre el precio actual del kWh para riegos agrícolas (p) y el precio tomado como referencia en su momento (p’).

Para una primera aproximación, puede tomarse p/p’ = 1.

El Sr. Agüera concluye que:

• El diámetro económico es independiente de la altura manométrica y de la longitud de la impulsión.

• El número de horas de funcionamiento es, con diferencia, el parámetro principal para el cálculo del diámetro económico.

Vamos a ver unos ejemplos que te permitan entender este método de cálculo.

Ejemplos. Se desea bombear desde un pozo a un depósito un caudal de 150 m3//h. Obener el diámetro económico y la velocidad para una utilización anual de:

a) 1.000 horas

b) 3.000 horas

f= 0,015 y η= 0,70

Solución a) 1.000 horas (hacemos p/p’ =1)

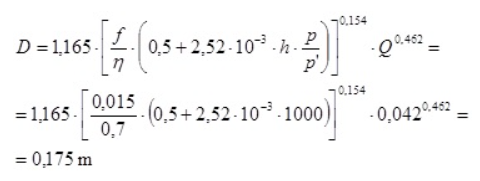
Podemos seleccionar una tubería de 150 mm o bien una de 200 mm. Elegimos finalmente una conducción de 150 mm, que es la solución que se adoptó en proyecto (velocidad económica del agua v = 2,4 m/s)

Solución b) 3.000 horas (hacemos p/p’ =1)

Seleccionaríamos una tubería de 200 mm. (v = 1,3 m/s). La influencia del número de horas de bombeo al año determina finalmente la elección de un diámetro mayor con respecto a la solución a.

Siguiendo con el ejemplo, supongamos que el precio actual de la energía sea el doble, es decir:

p = 0,1482

Solución a) 1.000 horas (p/p’ = 0,1482/0,0741 = 2)

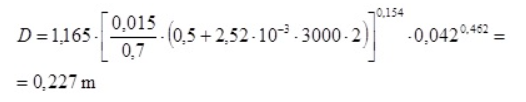
Podríamos seleccionar una tubería de 200 mm (v = 1,3 m/s) o bien de 250 mm (v = 0,85 m/s) ya que la solución se encuentra en la mitad. No obstante, y debido al costo de explotación –costo de la energía-, sería deseable elegir la tubería de mayor diámetro.

Para finalizar, comentarte que en la deducción de su fórmula simplificada, el Sr. Agüera consiguió prescindir de un término denominado coeficiente económico de ajuste, término que resultaba muy laborioso de valorar. Gracias a ello, se despeja enormemente la complejidad de cálculo y todo resulta más sencillo. 

En la sencillez precisamente se encuentra la esencia de las cosas que creamos, y esto, muchas veces, es lo más difícil de conseguir.